How to demystify π ?

In calculus there is a thing called Taylor Series which provides an easy way to calculate many irrational values to arbitrary precision. Pi/4 = 1 – 1/3 + 1/5 – 1/7 + …But this Taylor series is probably also one of the worst ways to generate PI on a computer. You have to have huge precision on your calculations and it’ll take many billions of iterations to get past 3.14159. Next try could be the use of atan, trouble is, the Taylor series for atan (PI/4 = atan(1) = 1 – 1/3 + 1/5 – 1/7 + 1/9… )converges very slowly for values of x near one, and it converges extremely slowly when x is equal to one.So how we did it: with the AGM calculation of Pi. In 1799, Gauss was startled to discover that his arithmetic-geometric mean connected, the half-circumference of a curve known as the lemniscate, with π, the half-circumference of a unit circle. procedure TBigFloat.PiConst(const MaxSig: TMaxSig);begin self.CheckPiPlaces(MaxSig);end; procedure TBigFloat.CheckPiPlaces(const MaxSig: TMaxSig);var localPrecision: word;begin localPrecision:= MaxSig+2; if localPrecision>zpi.sigdigits then calculate_PI_AGM(localPrecision+5) else begin self.Assign(zpi); self.RoundToPrec(MaxSig); end;end; Then we compare the result of the code with the wolfram alpha link above to make sure we get the right 1000 places in it: writeln(‘sha test1: ‘+sha1tohex(synsha1(tostring(normal)))); writeln(‘sha test2: ‘+sha1tohex(synsha1(PI1000))); >>> sha test1: b7805c4fb1662666d7741fa8f915daacf706cd01 >>> sha test2: b7805c4fb1662666d7741fa8f915daacf706cd01 Got it. So why doesn’t Pi have a 0 in its first 30 digits? 3.141592653589793238462643383279502884

Let’s assume (likely but is not proven at present) that Pi is a Normal Number¹. Amongst other things, this means that the frequency of occurrence of any digit in its decimal range is precisely 1/10. This assumption is in accord with statistical analysis of many trillions of decimal places of Pi. We can use this to calculate the probability that there are no zeros in the first thirty digits of our π; In order for this to happen, zero cannot appear in the first place, a probability of 9/10 and also not in the second place, also a probability of 9/10 and so on. We get the overall probability to be: (9/10)^30 = ˜ 4.24% //4.23911 So it is unlikely that no zero (or another selected number) appears in the first thirty digits.Can we say there is even less of interest in the decimal digits as a particular transcendental number, except that so many people think there is something special about it, for example you find your birth date (as 8 digits) in it.What can we do? We can count the frequency of each digit of Pi to assume a uniform distribution and independence and non predictability of each digit:

Piconst(10000) writeln(‘zero count: ‘+ itoa(StrCharCount(toString(normal), ‘0’))); for it:= 0 to 9 do println(itoa(it)+‘count: ‘+ itoa(StrCount(toString(normal),+itoa(it)[1]))); ref: zero count: 9680 count: 9681 count: 10262 count: 10223 count: 9764 count: 10125 count: 10476 count: 10237 count: 9718 count: 9489 count: 1014 But wait a second. Why does zero lag behind in the count. It is a perfectly non number digit? Just had to ask, its a rhetorical question. Lets check it with only 1000 digits: zero count: 930 count: 931 count: 1162 count: 1033 count: 1034 count: 935 count: 976 count: 947 count: 958 count: 1009 count: 106 for it:= 0 to 9 do FormatF(‘%d count: %d’,[it,StrCount(toString(normal),+itoa(it)[1])]); Obviously, some digit will lag. Which digit has a reason to lag? None has a reason to lag. Zero is none. Therefore, zero lags. — Larry Hosken This means as said before that each number is equally likely to be the next number so each has a 1/10 chance. Therefore, the occurrence of each digit should be equal once we reach an infinite number of decimal places. http://www.eveandersson.com/pi/precalculated-frequencies But Pi is obviously going to look different if we calculate it in base 8 or base 12 or any base other than 10. I was also reading a recent blog post by Evelyn Lamb where she mentioned in passing that 314159 is a prime number and that made me curious how many such primes there are. https://www.johndcook.com/blog/2018/09/04/pi-primes/ Formulas for prime-counting functions come in two kinds: arithmetic formulas and analytic formulas, see appendix prime-counting.

Prime-counting

def is_prime(n): if n>1: divs=[k for k in range(2,n) if n%k==0] return len(divs)==0 else: return False def nth_prime(n): primes=[p for p in range(n*n+2) if is_prime(p)] return primes[n-1] NativeWriteln(‘Start with maXbox4 Console Output—>’); for it:= 1 to 50 do if IsPrime(it) then NativeWriteln(IntToStr(it)+‘ is prime’); NativeWriteln(‘—–end—–‘); FreeConsole(); This is OK if you are just wanting to display output into the command line. But operations like redirecting output into a file for example are not working e.g.: start /wait Checker.exe > out.txt would still output into console and not into file out.txt. Different solution exists for PowerShell: If you are lost into the source code then you could easily add parameters to your app to write output to a file instead of the console: -o out.txt, since it’s your tool doing the writing, you can build wherever you want for example to start out of the shell and get output to the shell and in the end plot an image to another file output as a graphic like below: Call the script from the shell with>>> .\maxbox4.exe ..\examples\866_native_console.txt The script can be found: http://www.softwareschule.ch/examples/1093_XMLUtils_Tutor92tester.txt http://www.softwareschule.ch/examples/866_native_console.txt Author: Max Kleiner Ref: http://www.softwareschule.ch/box.htm https://scikit-learn.org/stable/modules/ Doc: https://maxbox4.wordpress.com >>> from geopy.geocoders import Nominatim>>> geolocator = Nominatim(‘maxbox-app’)>>> place,(lat,lng) = geolocator.geocode(“Breitenrainplatz 2 Bern”)>>> print (“%s: %.5f, %.5f” % (place, lat, lng)) Release Notes maXbox 4.7.6.10 IV Jan. 2022 mX476 ************************************************** Add 25 Units + 6 Tutorials Total of Function Calls: 35371 SHA1: of 4.7.6.10 A2B2B2D1596C6A5F3ACCED90D0C2246172A3DE2CCRC32: 285ACBCB 31.3 MB (32,921,928 bytes) ZIP file maxbox4.zip sha1 E267EB40AA945AD10B88EF8274C837F510DD96D4 https://www.virustotal.com/gui/file/3080a507b536ff12ec70e9a8df9eba27aca5c90709d73f42a5ad02211342bd64/details

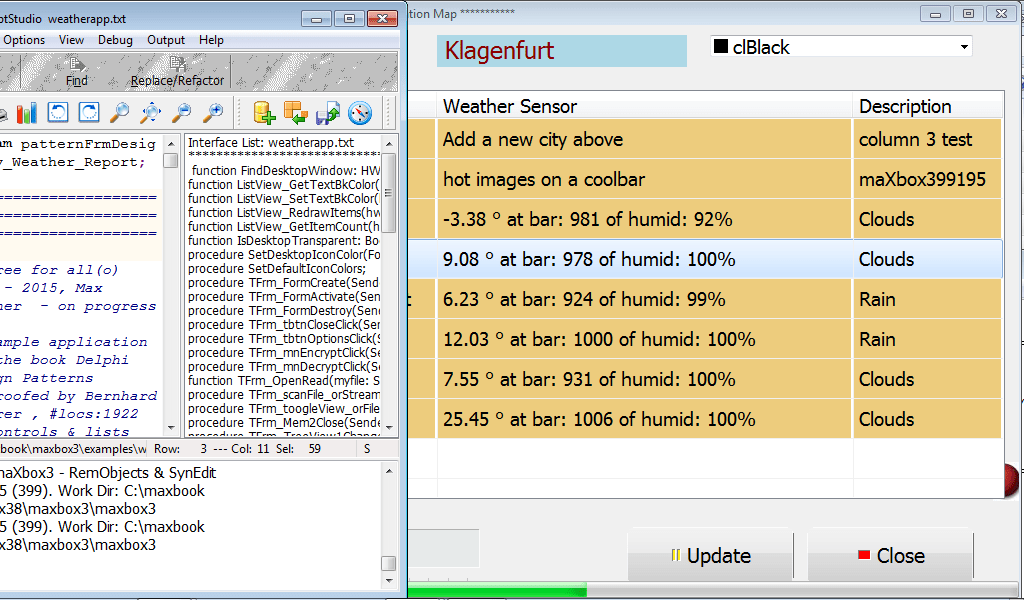
How to produce an NFT (non fungible token) from an EXE:

1. Convert the EXE to a PNG with this Java Tool:

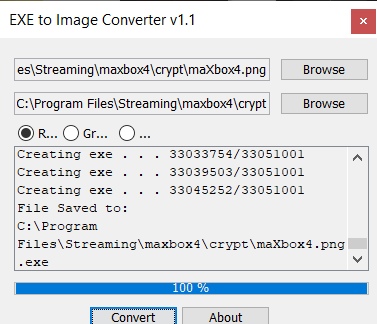
2. Publish the PNG to opensea.io

maxboxexe4png – maxbox | OpenSea

3. Check the token in your wallet

OpenSea: OPENSTORE Token | 0x495f947276749ce646f68ac8c248420045cb7b5e (etherscan.io)

TokenID: 91607934750905988430739577239694576301564617410208701007294593060155848392705

MD5: 945a72002eb4608a94b5ddc5c79c6f6e

SHA-1: e9e4eb97fb2f65c8025f78e29df07cab0b61e740

SHA-256: 2649e7f1b49025a3ede32cc3b4f68b492155eb4aeb14b639ec71ebc41edc007e

SSDEEP: 786432:mUwaZjA3tneMUTWFuwH64NDYVqeUrpUVLUsk6oLq9uEV16ivG6MK/R8lvf9f94ii:rwae3tnemhaW9eW4LUtrqt19vGdKmpFQ

TLSH: T194B733D056EBFAC5B1563673B38270167102C9ABC5EF29A9563DDB1830CA040EE7F9E1

File type: PNG

Magic: PNG image, 5749 x 5749, 8-bit/color RGB, non-interlaced

TrID_ Portable Network Graphics (100%)

File size: 47.89 MB (50213248 bytes)

Model-Code-Test-Document IT

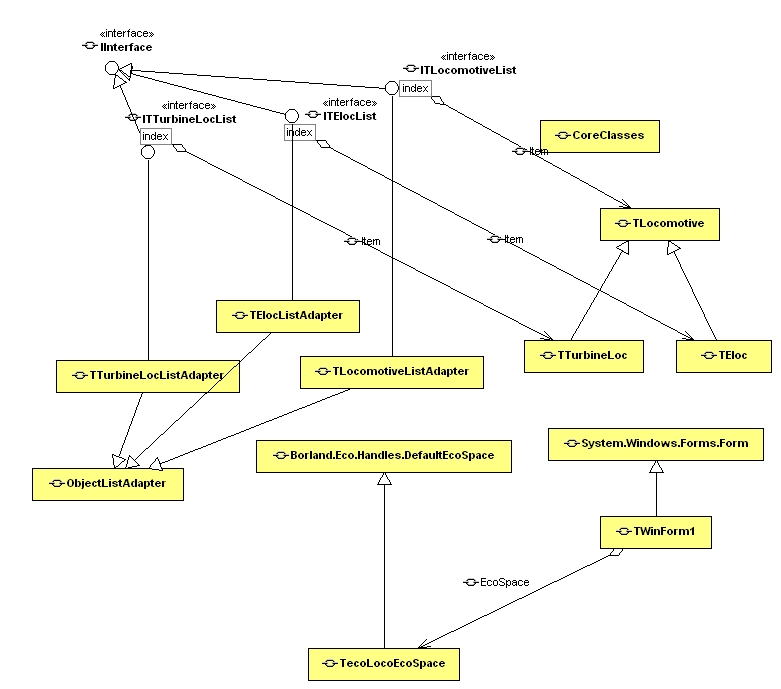
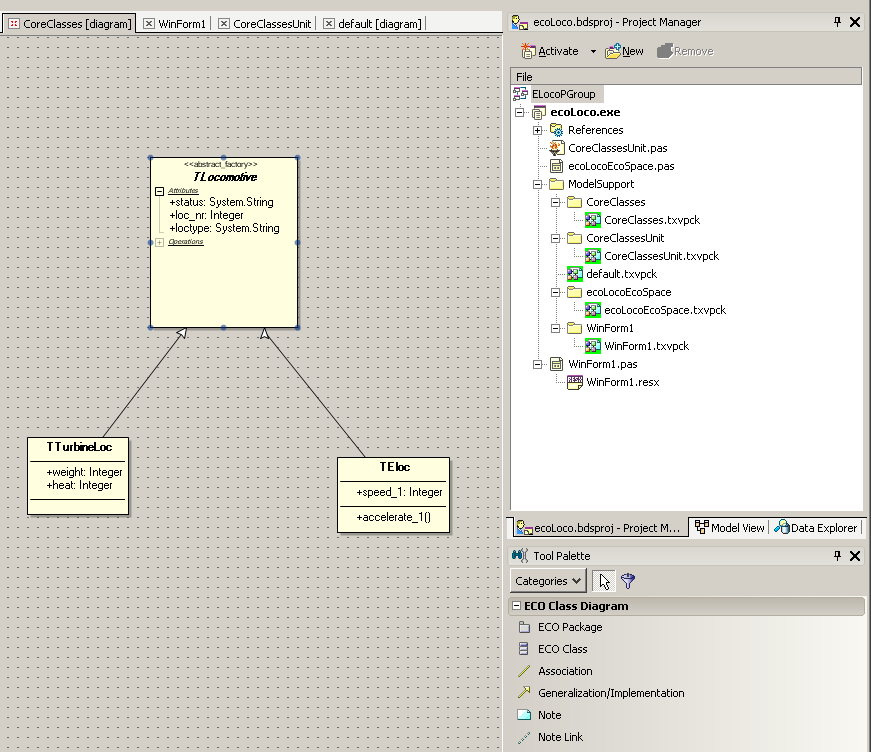
ECO Modeling

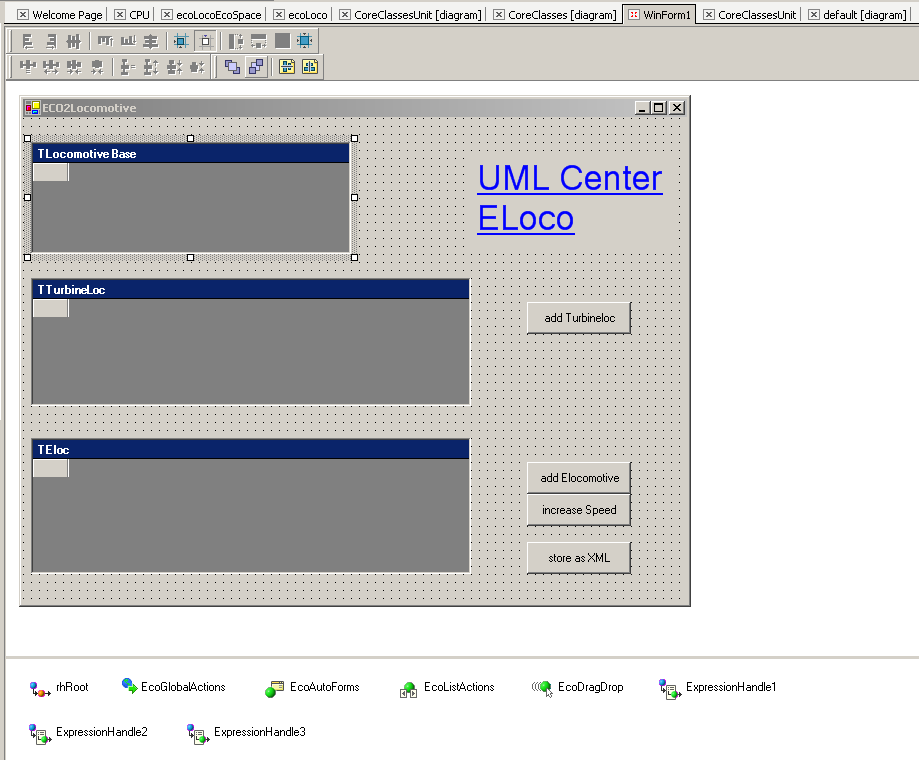
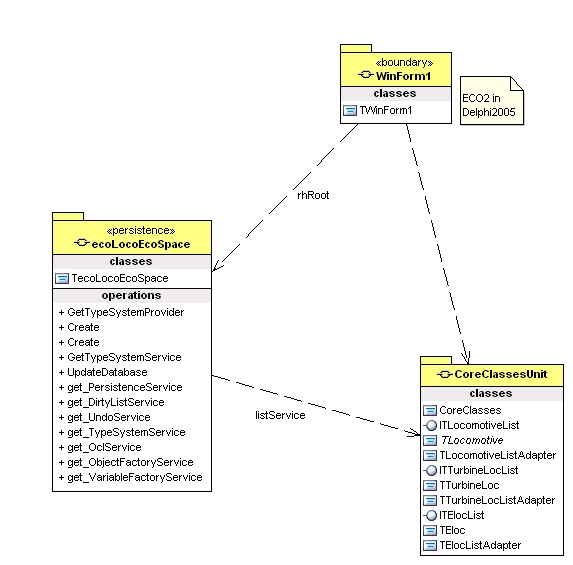
In this report, I want to use model-driven to show you how to set up a persistent and object-oriented application with Delphi 2005 and ECO II. The automatisms of the MDD (model driven development) in ECO are an enormous support for business objects or data-intensive systems, especially since ASP.net pages or web services can also be generated with it.

1.1 Entry with class ECO (stands for Enterprise Core Objects) enables the implementation and control of an MVC (Model View Controller) architecture, i.e. a middle layer of control classes (presentation, mapping and handles) mediates between the business objects and the graphical representation. In addition, ECO offers sophisticated database handling that, in addition to “class to table mapping” in a relational database, will also allow cached updates and transaction handling in the future.

Memory Manager Test

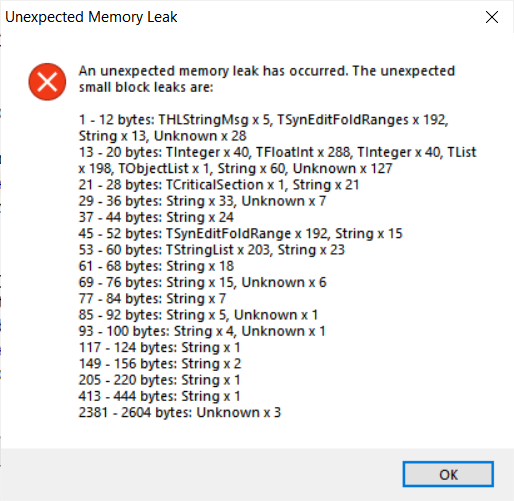
procedure TestTObjectList;
var  objl: TObjectList; i: integer;
begin

 objl:= TObjectList.Create1(True);
 objl.OwnsObjects:=true; 
  
 writeln('capacity '+itoa(objl.capacity));
  
 for i:=0 to 1500 do begin {o:= TObj.Create();} 
  //objl.Add(TStringStream.create('this is a smart stream')); end; 
  objl.Add(TStringStream.create(filetoString(exepath+'firstdemo.txt'))); 
 end;
      
 writeln('capacity '+itoa(objl.capacity));
 writeln('count '+itoa(objl.count)); 
 writeln('last func:'+objtostr(objl.last)) 
 writeln('items last '+objtostr(objl.items[1500]))
 //function IndexOf(AObject: TObject): Integer; inline; 
 writeln('idx of: '+itoa(objl.IndexOf(objl.last)));
  
 objl.Clear;
 objl.Free;
  
end;  

capacity 0
capacity 1695
count 1501
last func:TStringStream@0AEE0130
items last TStringStream@0AEE0130
idx of: 1500

Now the same code without free of the objects. Use this one to specify if you want the list to own its content (means: it takes care of destroying an item when it is removed from the list or the list is destroyed) or not. The constructor without parameter (which you probably used) sets this to true. Now we set it to false (objl.OwnsObjects:=true; )and compare.

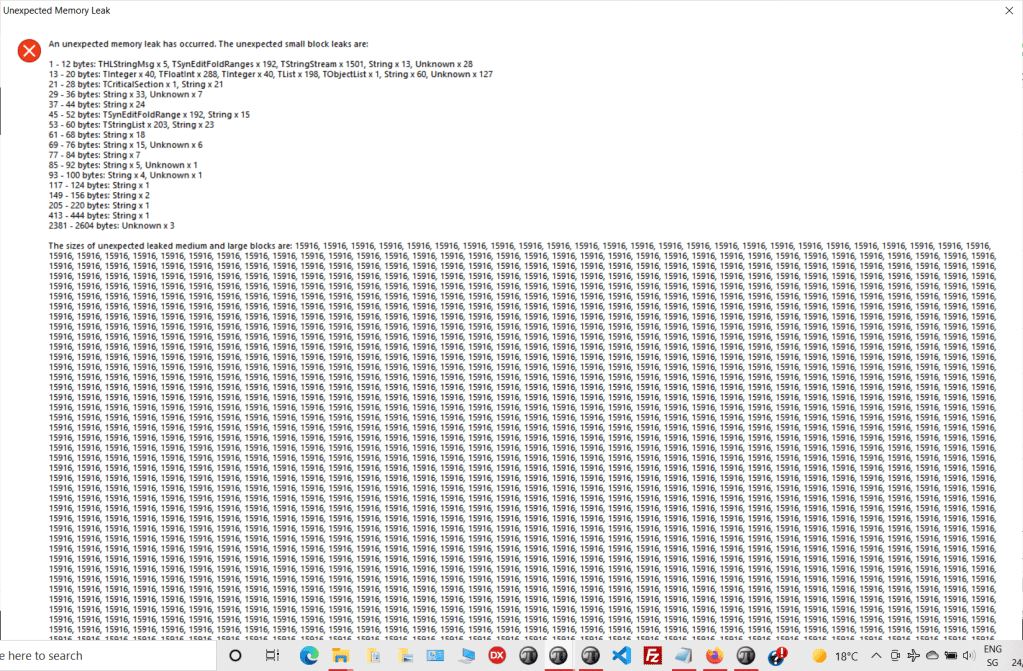
This is due the filetoString(exepath+’firstdemo.txt’) so each file on the StringStream object allocates 15,914 bytes on the objectlist.

When I set the ‘OwnsObjects’ property to true and then attempt TObjectList.Free, sometimes (not always) I get an ‘invalid pointer | operation’ error.
| Any clue?
If you have already freed, but not nilled any of the items in the list, then
this will cause an AV when the list tries to free it a second time.